Illustrating this symmetry group is a little more complicated, so in the animation, we will mostly move around triangles made up out of three copies of the basic tile or fundamental domain shown above on the left. Let's call this tile a "kite".

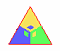We can rotate this tile twice by 120 degrees to obtain the triangle shown to the left. We have color coded the three copies of the kite tile to make them easier to see. Using the reflections in p31m, we then wallpaper the plane by reflecting the triangle over its three edges. Take a moment to convince yourself that we end up constructing the same tiling with the triangle as we would if we wallpapered with the three times as many kite tiles by reflecting them about their red edges and rotating about the marked corner.

The tiling as a whole has reflexive and 3-fold symmetry as you can see by reflecting it across any red line, or rotating by 120 degress around any of the points where reflection lines meet.

When imagining shifting the tiling as a whole, you have to take the coloring into account when trying to decide if the shifted tiling matches up with the original. It is okay if one kite lands on another kite of a different color, but only if all the colors are shifted in the same, systematic way.

The thing to pay attention to is the order of the colors as you go around a triangle. For example, if the blue kites wind up on top of yellow kites, then yellow kites must end up on green kites. In other words, all the colors must shift in the clockwise direction as you go around one of the triangle. This is important, since there are actually ways of picking the tiling up and puttting it back down again so that the order the colors are in gets reversed as you go clockwise around a triangle. Can you think of one of these "color orientation" reversing transformations?

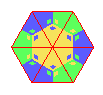As with all of the wallpaper tilings, p31m tilings are periodic, which is the same as saying they are symmetric under translations. To see this, use the p31m symmetries to constuct the tile shown on the right. We can use just translations to wallpaper the plane with this tile to obtain the original tiling.

Kali denotes this symmetry by "3*3". You can go to now to experiment with symmetry p31m.