As you can see from the animation, you build a p3 tiling from a rhombus shaped tile, like the one shown on the left, by reflecting the rhomb by 120 degrees about any of its four corners. At the corner with the obtuse angle, rotating produces three copies of the rhombus, which meet to form a hexagon. On the other hand, at the corners with acutes angles, rotating by 120 degrees leaves a gap between every other tile. These gaps are filled by a second set of three tiles, which are also all 120 degrees apart from each other.

Imagine you rotate the entire tiling by 120 degrees about any of these corners. You see that the rotated tiling matches the original perfectly - it is as if the tiling was never moved. We say the tiling as a whole has 3-fold symmetry.

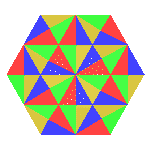Surprisingly, even though p3 tilings are contructed using only rotations, they also have translational symmetry. If you rotate a copy of the original tile around one of the red/green corners three times, you get a hexagon like the one shown on the right. You can then wallpaper the plane with this hexagon using only translations, recreating the original tiling. See if you can visualize how this works!

Kali denotes this symmetry by "333". You can go to now to experiment with symmetry p3.