One of the first thing that comes to mind when people think of tilings
are repeating patterns. Tile floors, mosaics, and brickwork generally
all display some kind of repeating pattern. In mathematical language,
a pattern that repeats in a regular way is called periodic.
Periodic vs. Repeating Tilings
 Imagine walking in a straight line across a tile floor. As you walk,
you notice that you keep seeing the same pattern again and again. In
ordinary language, we might say that the pattern repeats.
Imagine walking in a straight line across a tile floor. As you walk,
you notice that you keep seeing the same pattern again and again. In
ordinary language, we might say that the pattern repeats.
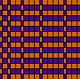 In order to say that the tiling is periodic, as opposed to merely
repeating, a mathematician would want to be sure the repetition
happens in a regular way. If you were to walk from left to right
across the the tiling shown on the right, you would keep seeing the
thin tile again and again, but the repetition isn't at all regular,
since the distance between occurences of the thin tiles keeps increasing.
In order to say that the tiling is periodic, as opposed to merely
repeating, a mathematician would want to be sure the repetition
happens in a regular way. If you were to walk from left to right
across the the tiling shown on the right, you would keep seeing the
thin tile again and again, but the repetition isn't at all regular,
since the distance between occurences of the thin tiles keeps increasing.
On the other hand, if you were to cross the tiling from top to
bottom, instead of left to right, the pattern would repeat
regularly. So we also need to be sure that a tiling is as regular as
possible in all directions, before declaring it is periodic. In
general, it a hard to say what "as regularly as possible" means in a
precise mathematical way. But for a plane tiling, it basically means
that the tiling repeats in two independent directions, since the plane
is 2-dimensional.
A Test for Periodic Tilings
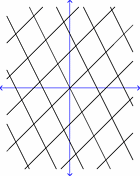 So how can we tell if a tiling is periodic? One way is to construct a lattice. A lattice is a grid
consisting of two sets of evenly spaced parallel lines. In the image
on the left the lattice is the black lines (the blue lines represent
the cooridinate axes in the plane).
So how can we tell if a tiling is periodic? One way is to construct a lattice. A lattice is a grid
consisting of two sets of evenly spaced parallel lines. In the image
on the left the lattice is the black lines (the blue lines represent
the cooridinate axes in the plane).
By the way it is made, you can see that a lattice repeats regularly
in two directions. The parallelograms formed by the lattice are
called period parallelograms. A
tiling is periodic when we can lay a lattice over the tiling in such a
way so that the period parallelograms contain idential pieces of the
tiling. We call these pieces fundamental
domains for the tiling.
To see how this works in a specific example, consider the sequence
of images below. The picture on the left shows the tiling. The
middle pciture shows the tiling with a lattice superimposed on it.
The picture on the right is a close up of a fundamental domain.
You can easily see how given a single fundamental
domain, we can recreate the periodic tiling by translating and
pasting. We just translate copies of it in the two directions given
by the lattice.
Fun with Fundamental Domains
An interesting thing to notice about fundamental domains is that
they are not unique. For example, given a lattice we can combine two adjacent
fundamental domains to
obtain a new fundamental domain.
The rectangle on the right below is a closeup of the fundamental
domain obtained by taking two
copies of the original fundamental domain from above and combining them.
It is the fundamental domain coming from the larger lattice shown
below on the left.
We have produced two fundamental domains. Are there more?
Indeed, yes! There are many more. Look at the
period parallelograms of the lattices below the right and
left. Can you convince yourself that these period parallelograms are
also fundamental domains of the tiling? Can you see how to find other
fundamental domains?
Next on the Menu: Symmetry
In discussing periodic tilings, we encountered the idea of building up
a tiling by translating copies of a fundamental domain all over the
plane. In this case, the rules for how to move the copies of the
fundamental domain are pretty clear -- just slide the copies in the
directions parallel to the lattice lines.
However, this is just the tip of the iceberg when it comes to
building up tilings from fundamental domains. Different sets of rules
for shifting around fundamental domains lead to tilings with intricate
and beautiful symmetries.
|

