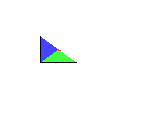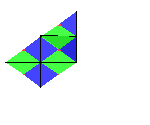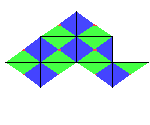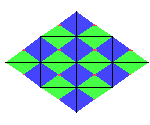 The ninth, or cmm symmetry contains perpendicular reflections and
half-turns (180 degree rotations).
The ninth, or cmm symmetry contains perpendicular reflections and
half-turns (180 degree rotations).
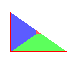 To build a cmm tiling,
begin with the tile on the left. Rotate the tile about the red point
and reflect it across the red lines. To build a cmm tiling,
begin with the tile on the left. Rotate the tile about the red point
and reflect it across the red lines.
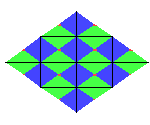 If we rotate the entire tiling 180 degrees about any of the red points
the rotated tiling will match the original tiling perfectly.
Because of this, we say the tiling contains two-fold rotational
symmetry. If you look closely you will see that the tiling
also lands back on top of itself if you rotate by 180 degrees about points where the
vertical and horizontal lines of reflection intersect. Those of you
who know a bit about isometries you will
realize that this is because each rotation
is a composition of reflections.
If we rotate the entire tiling 180 degrees about any of the red points
the rotated tiling will match the original tiling perfectly.
Because of this, we say the tiling contains two-fold rotational
symmetry. If you look closely you will see that the tiling
also lands back on top of itself if you rotate by 180 degrees about points where the
vertical and horizontal lines of reflection intersect. Those of you
who know a bit about isometries you will
realize that this is because each rotation
is a composition of reflections.
The cmm tiling shown above is also symmetic with respect to
reflection. That is if we reflect the entire tiling about one of
the horizontal/vertical lines of reflection then we get the same
tiling again.
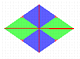 Suppose we reflect the original tile from above to obtain the larger
rhombus shown to the right. Since a rhombus is a parallelogram we can
use the p1 symmetry, that is just the translations, to wallpaper
the plane with this new tile. This new tiling will match the original
cmm tiling, and so cmm tilings are also symmetric with respect to
translations.
Suppose we reflect the original tile from above to obtain the larger
rhombus shown to the right. Since a rhombus is a parallelogram we can
use the p1 symmetry, that is just the translations, to wallpaper
the plane with this new tile. This new tiling will match the original
cmm tiling, and so cmm tilings are also symmetric with respect to
translations.
Kali denotes this symmetry by "2*22". You can go to  now to experiment with symmetry cmm. now to experiment with symmetry cmm.
| 
