Transformation formulas make computer animations possible by giving a way of automatically updating the positions of points and polygons. The most useful transformations, called isometries, are those which do not distort shapes and sizes. Ideally, an animator should have complete list of all isometries and their formulas at his or her disposal (most likely built into software).

A good way to start such a list is to consider the isometries we are familiar with from our day to day experience. Think of picking up a paper square on a table top and putting it back down. The end result will be some sort of isometry applied to the square; unless you crumple it up, its size and shape will not be distorted by the transformation that moved it from its original location, and hence we deduce it must be an isometry.

A moment's thought ought to convince you that there are really only four fundamentally different ways you can move a shape on a tabletop:

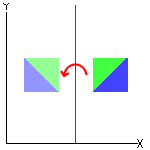Reflection	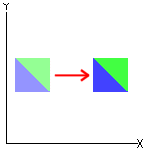Translation
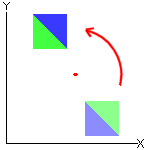Rotation	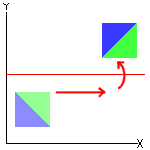Glide Reflection

Of course, there might be some other tricky isometries hiding somewhere. For example, what do you get if you translate and then rotate? Since neither transformation alone distorts the square, doing one after the other won't either, and hence the combination must be an isometry as well. But is it again one of the isometries on our list, or is it something new that we have missed?

Before we can resolve this mystery, and ask the real isometries to stand up and show themselves, we need to become better acquainted with our prey...

Next: "Translation"