Penrose tilings are a class of beautiful and fascinating nonperiodic
tilings. In addition to their intristic beauty they possess an
intriguing mathematical structure. This structure is helping
scientists studying crystalography understand quasicrystals,
a new breed of strange high-tech materials discovered in 1984 by
looking at X-ray diffraction patterns. For more information about
quasicrystals, consult Marjorie Senechal's book Quasicrystals and Geometry.
 is a fun way to learn more about Penrose tilings
and other "quasi-periodic" tilings. Using QuasiTiler, you can create
many tilings, including the Penrose tiling above.
What's the Big Hullabuloo?
Penrose
tilings, invented by Oxford mathematician Roger Penrose and author of
the popular book The Emperor's New Mind, have made a
big splash in the math world in recent years, but you may be asking
yourself what the excitement is all about? Aside from being
beautiful, Penrose tiles are interesting because they always tile the
plane nonperiodically, even though they
can be constructed from just two tiles, following a few simple rules.
This caught everyone by surprise, because you would think that such a
tiling would turn out to be very symmetric, like the wallpaper tilings.
While Penrose tilings nonperiodic, at first glance they seem like
they ought to be periodic. If you look more closely, you will see
they are almost but not quite periodic. Mathematicians call such
tilings quasiperiodic. In a
symmetric tiling, you can shift a copy of
the tiling around so that it exactly matches up with the original
again. With a quasiperiodic tiling, you can can still shift a copy so
that it partly matches up with the original, but only right around
where you are doing the shifting. Further away, the tilings will
inevitably fail to match. Sometimes this is called local symmetry.
Constructing Penrose Tilings
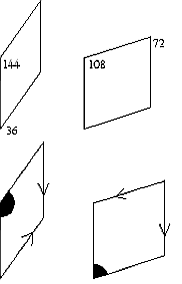Penrose tiling are constructed from two tiles, with very specific
shapes, illustrated on the left.
Each tile is a rhombus or
"rhomb" for short. The thin rhomb has angles of 36 and 144 degrees.
The thick rhomb has angles of 72 and 108 degrees.
Looking at the tiles you may be confused. The whole point of a
Penrose tiling is that the tiles should always tile the plane
nonperiodicly, but there are several obvious ways to use these rhombs
to make periodic tilings. Can you see a way to make a periodic
tiling? (Hint: make it periodic in only one direction).
Even though we can use these rhombs to make periodic tilings, there is more to a
Penrose tiling than just the shapes. A Penrose tiling must also
follow rules which dictate how you can put the rhombs
together. The key to the Penrose rules is the bottom illustration to the
left. The rules themselves are:
When constucting a Penrose tiling, two adjecent vertices must
both be blank or must both be black. If two edges lie next to each
other they must both be blank, or both have an arrow. If the two
adjacent edges have arrows, both arrows must point in the same
direction.
Once again, we should stress that just using the rhombs alone do
not necessarily give you a Penrose tiling. For a Penrose
tiling, you have to use both both the rhombs and and the
rules.
Method In the Madness
|
Though this be madness, yet there is a method in't.
|
| |
Hamlet,
Act 2, Scene 2
|
The Penrose tilings are one of the more enchanting objects to be found
in geometry. We are first lured by the tilings' disoreinting
nonperiodicity and then captured by the regularity lurking within this
chaos.
Keep your eyes open for "Method in the Madness," a Science U feature
article on the mathematics behind Penrose tilings. Coming Soon!
|
