Dissection Problems in History

Just before the turn of this century, mathematicians began holding an international congress. During the second such international congress, held in Paris in 1900, a famous mathematician David Hilbert read a list of mathematical problems. These problems where tremendously influential, and partly as a result, Hilbert is now one of the most prominent mathematicians in history.

Hilbert had a very broad and profound knowledge of mathematics and physics, and he thought of 23 problems, posed as challenges, might be a good motivation for mathematical research in the new century. Most of the problems he proposed were aimed at developing general programs. The third problem, however, was simple to state and understand, asking only if a counterexample to a theory could be found.

In 2-dimensional Euclidean geometry, areas of polygons can be computed by cutting them into pieces and pasting into polygons of know sizes, in much the same way that we illustrated the Pythagorean Theorem on the previous page. Hilbert did not believe that a general theory of volume can be based on the idea of cutting and pasting. In particular, he thought that it should be possible to find two tetrahedra with equal volumes with the property that you couldn't cut up the first one into tetrahedra and then reassemble the pieces to get the second one.

Here is a partial translation of his (more precise, and thus more difficult) statement of the problem:

"Gauss mentions in particular the theorem of Euclid that tetrahedra of equal altitudes their volumes are proportional as their bases. ... Gerling succeded in proving the equality of volume of symmetrical polyhedra by dividing them into congruent parts. Nevertheless, it seems to me probably that a general proof of the kind for the Euclid's theorem is impossible, and it should be our task to give a rigorous proof of its impossibility. This would be obtained as soon as we specify two tetrahedra of equal bases and altitudes which can not be split up into congruent tetrahedra and which cannot be combined with congruent tetrahedra to form two polyhedra which themselves could be split up into congruent tetrahedra."

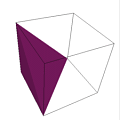
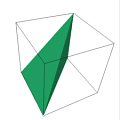
Some of Hilbert's famous problems have still not been solved, but not this one. Max Dehn found the solution a few months after it was posed. Surprisingly, it turns out that two fairly commonplace tetrahedra will work as the counterexamples Hilbert asked for. In particular, the tetrahedra pictured below, with vertices at

{(0,0,0),(1,0,0),(0,1,0),(0,0,1)}
{(0,0,0),(1,0,0),(0,1,0),(0,1,1)}