
|
|

|
|
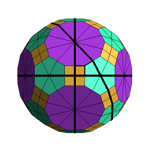
Which archimedean solids can't be generated with triangle tilings?


|
Info Center | Geometry Center | Library | Observatory | Studio | Store | Science Me
Page last updated Wed Jul 28 17:05:18 CDT 1999
Comments to webmaster@ScienceU.com
Copyright © Geometry Technologies 1999. All right reserved.



